University of Wyoming and Northern Colorado University

• Discrete and Combinatorial Mathematics (MATH 5700 - Summer 2012)
  For highschool teachers

University of Calgary

• Calculus I (Math 265 - Fall 2017)
• Linear Algebra (Math 211 - Spring 2017)
• Discrete Mathematics (Winter 2017)
• Linear Algebra (Math 211 - Fall 2016)
• Introductory Calculus (Math 249 - Spring 2016)
• Calculus I (Math 265 - Fall 2015)

Western Illinois University

• Calculus I (Math 133 - Spring 2015)
• General Elementary Statistics (Stat 171 - Spring 2015)
• Concepts of Mathematics (Math 101 - Fall 2014) > Student Comments
  • Dr. Monfared is very helpful and I can tell he cares about his students and enjoys coming to teach. Overall he is a very good instructor.
  • He is very helpful.
  • He's a great teacher.
  • Very helpful when you ask a question. I usually don't understand when he first explains it but I do after I ask questions about the worksheets. Readily available and open.
• General Elementary Statistics (Stat 171 - Fall 2014) > Student Comments
  • My Instructor does a great job of teaching.
  • He does very well teaching, and has the best teaching style I've seen for math. He gives plenty of handouts and explains everything clearly.
  • I think overall I have a good professor. Ive went to his office hours many times and he was helpful.
  • Very organized.
  • Great quality teaching.
  • Math usually isn't my subject, but Professor Monfared does a good job explaining everything. I really like the online homework and the worksheets we do in class together. Helps me learn the material easier with lots of examples that he helps guide us with and helps with homework.
  • I like the way of learning because he teaches, we learn then we do multiple examples together in class and once it is time to do homework online, it is somewhat a breeze. He is always willing to help in class, after class and through email.
  • Clarity, encouragement, and helpfulness.
  • He is a great teacher. He takes it slow enough for everyone to understand. He will help you when asked and is always willing to extend the homework if you need more time to get everything right.
  • Professor Monfared is well prepared and very helpful. He presents the material in a way that is easily understood, and his tests and homework are fair.
  • The worksheets handed out in class are a big help.
  • Overall I enjoy the class.
  • He was good and knew what he was talking about.
  • He is so helpful for me.
  • My instructor is very helpful and if I need help he will quickly respond to my emails. He seems to want everyone in the course to do well.
  • He gave worksheets to follow during class and allowed me and other to actually participate. This was very helpful and he should continue for future classes.
  • Things that I did find helpful are the written homework, and his openness to questions. He just wants you to have an understanding and clear knowledge of the subject rather than just getting you through the course as quick as possible.
  • The worksheets help significantly.

University of Wyoming

• Elementary Linear Algebra (MATH 2250 - Summer 2014) > Student Comments
  • After the first week when i asked more questions I started learning more and I think it's effective. I could do the things I understood and when it got hard, class time was utilized efficiently to understand more what was going on. The assignments were a lot to do but its a summer class. It should be that way. It was not too much to where I was inundated but enough to keep my focused and in a learning mode.
  • Keivan's teaching method was having us watch and read the class materials before we covered them in class. I liked this approach as it allowed nearly the entire class period to be open for questions if we had problems.
  • I felt like Keivan did a great job teaching this course. We used effective technology. I really liked the supplemental lectures from MIT. It really helped with understanding. But over all, I think that this class really challenged me. Keivan, Thank You! I really enjoyed the course!
  • I liked the setup of the class. Although it was a lot of work outside of class time I found the videos and worksheets helpful.
  • The course has been a fantastic introduction to Linear Algebra, and its many applications. The book was (in my opinion) the best textbook I have read to date. The setup of the class with the preassigned topics and then working problems and concepts was the optimal way to learn the material. Thank you for an informative, and fun class.
  • Keivan did a great job applying the topics needed to understand and comprehend linear algebra. The course load was quick, but maintained a pace that allowed for the full grasp of the topics needed to move on. I think the homeworks and tests applied a good amount of the knowledge learned while keeping the course challenging.
  • Overall the semester went well. I understand that there was A LOT of material to cover in just 6 weeks; watching the videos every single night was alright.
  • Keivan was a great instructor. He was extremely helpful in class and always explained things in a clear manner. The assignments were very helpful in cementing what the video lectures and book were teaching. Everything was done extremely well.
  • I want to say that I really enjoyed the class.
  • I felt that Keivan did a great job in a short amount of time, with difficult material, and a class with very diverse experience.
  • I enjoyed the format of this course in which we watched the lecture outside of class, took a quiz at the beginning of class, received a short overview of the lecture, and then worked problems in class. Working problems in class helped reinforce the material and if we had any questions, Keivan was always willing to help. I thought the tests, homeworks, quizes and make up policy for the quizes were very fair.
• Geometry and Measurement (MATH 2120 - Spring 2014)
  For elementary school teahers
• Calculus III (MATH 2210 - Fall 2013) - Discussion Leader > Student Comments
  • Overall Keivan was extremely helpful.
  • Keivan was very helpful. I went to his office hours four or five times. He helped clear up my struggles. And he did a great job leading discussion and helping students.
  • Great teacher. Always provides helpful information to help the student to solve their problems.
  • He did a good job in answering the students questions and any topic that wasn't covered during the class.
  • Keivan is awesome.
  • Keivan was great.
  • Hands down the best teacher I have ever had for a class in college, basically became friends with him and he taught me almost all of Calc 3.
  • Very helpful and very understanding of the material. One of the best, if not the best, math instructor I have ever had at UW.
  • Very helpful and knowledgeable.
  • He was helpful. Knows the material and is almost always able to explain it in an easy way.
  • Keivan was an excellent teacher, he was the best teacher I have had at UW thus far. He was kind, knew his material very well, and was committed to fully answering any and all questions during discussion. He clearly made himself available for students wanting to meet for questions above and beyond the requirements and always brought a positive and helpful attitude to any meeting or discussion.
  • Very effective! Did a good job on making it challenging.
  • He is a very nice guy and enjoys teaching. He seems to really care about his students and help them out.
  • He was very helpful when he would go over material.
  • Keivan was a great teacher to have, and from conversations with other students, I feel like he did a better job in my discussion than others. He was very knowledgeable over the topics in class and knew more than needed to teach this subject.
  • He was very helpful with the questions I had about any of the problems.
  • I liked how Keivan sometimes explained problems in a different way - this sometimes helped me understand difficult concepts. I might've preferred working through problems as an entire class as opposed to in small groups, however.
  • Keivan Monfared did an excellent job of breaking down problems into easily understandable and manageable concepts. He also did a good job in summarizing the chapter we would currently be working on and Keivan was always good at going over challenging problems on there one-on-one if needed.
  • Keivan performed well when addressing topics with the class and always worked with students as they needed, including offering different ways of approaching or thinking about a problem. the discussion material has proved to be exceptionally invaluable to me.
  • Keivan was extremely helpful. He does a very good job of explaining difficult topics in ways that are easy to understand. Without his help I would not have nearly the understanding of the material that I do now.
  • was very good as explaining things at the correct level.
  • Had some really innovative ideas to get the class to mingle and partner with people they wouldn't usually work with. Was knowledgeable and helpful with the subject matter.
  • He ran an effective class. It was well ran.
  • he was fun and helpful in every class and he showed good understanding of the subject
  • Keivan is an incredibly intelligent teacher who really is able to explain Calc III in a way that I understand. I think he is incredibly helpful, and I think he should be a professor.
  • I liked that Keivan could explain the material in more than one way. I feel like that is hard to come by, especially in math. He was very helpful and I learned the material better in his class because he led us through examples and could give an explanation of the problem.
  • Keivan was generally very helpful.
  • Keivan is a very helpful instructor and helps us to understand the material by explaining it in simpler terms.
  • He is a great teacher, he really understood how to do the math and always was able to help with the questions we asked.
  • Keivan was always knowledgable and helpful
  • Keivan truly wanted us to succeed, knew his material, and knew how to explain it. He was engaging and helpful.
  • He seemed well organized and knew the material. He had us to get into groups which increased our interaction with each other. He answered questions well and helped when needed.
  • keivan is going to be a great teacher in the future. always very organized and helpful. I learned far more from keivan than others.
  • Keivan not only understands the material extremely well, but he is very skilled at teaching the material. He is also very good at getting the class to discuss with one another.
  • describes things in multiple ways which is VERY helpful for understanding.
  • Keivan was very helpful and always answered my questions as clearly and effectively as he could. He seemed to care a lot about student success and offered great advice. He would explain details about integration that didn't make sense until he did. Also, he drew effective drawings on the chalk board that helped illustrate what was going on, which made everything clearer.
• Calsulus III (MATH 2210 - Summer 2013) > Student Comments
  • Professor Monfared was thoroughly effective at teaching multivariable calculus. He assigned useful work, provided useful material, work plenty of examples, and was always accessible in the math lab on certain days of the week. My favorite part of his teaching style was the time he took to do reviews before exams and worked even more examples even though he already did many in class. He cares whether or not his students understand the material. He is also very effective at explaining very complicated material the course so often presented. Fantastic course.
  • Good professor and teaching methods
  • This was a good course with good teaching methods he easily showed his teaching methods and the content in the class was relayed very well
  • Good explanations
• Algebra and Trigonometry (MATH 1450 - Spring 2013) > Student Comments
  • Mr. Monfared is an excellent instructor. He taught this class very well, and to the best of his ability. He is a great value to the university and mathematics.
  • Good teacher. Very approachable!
  • The instructor is very smart! He has very good teaching methods,a very effective teacher
  • Overall Keivan was very helpfull, and i visted him a couple times in office hours and every time i did he was exellent at helping me. The course overall was challenging But overall it was a really great job on Keivans part.
  • Keivan is a great teacher. He expalins well and he know how to reach to students' minds. Also, he explains easily which it is the primness ways for students. He has a good knowledge of mtah. He has many ways for explination.
• Calsulus I (MATH 2200 - Fall 2012) > Student Comments
  • Keivan is an effective teacher. Keivan is doing great.
  • Keivan is a great teacher. He knows the material very well, and is good at understanding and answering questions. By far, he is the most interested of all my teachers in an individual's progress. I'm very pleased with Keivan's instruction.
  • He is a very dedicated teacher always putting in effort out of class for students. I've seen him in Mathlab and although I haven't gone to his office other than to take a test I know he is available a lot of the time. His teaching methods are great. If you go to class and pay attention you can do well, but the webassign also helps with the basic calc concepts. The SI sessions before tests really help.
  • Keivan is a very intelligent man, he was very helpful.
  • The online homework was a great help.
  • Always very helpful and seemed to care about the students grades.
  • good
  • he did a good job.
  • Keivan was an excellent teacher. Unlike many professors, he took interest in his students. When I missed class several times and did poorly on a test, Keivan showed genuine concern and even asked me personally if I was doing alright. He made calculus easy to understand, and his lectures were helpful and intuitive. As a professor, Keivan receives a 10/10 in my book.
  • Keivan is a good teacher. He was very helpful and always willing to go over examples, or explain where he got a certain answer.
• Calculus II (MATH 2205 - Summer 2012) > Student Comments
  • Very effective and simplistic explanations and presentation that enables all of the students to understand important concepts of Calculus II.
  • I thought he was a good teacher.
  • He was very good. He knew what he was teaching.
  • The instructor was great! With the limited time available in the summer semester, he was proficient at covering the essential points of the class. He always asked if we understood the material and helped me out several times with tricky problems. I would definitely recommend Kevian to anyone taking Calculus 2 in any semester.
  • First, I would like to say how impressed I have been with the quality of instruction from the grad students in the math department. Out of the five classes I've taken with five different instructors, four of them have been par or above. Let f(x) be the ratio of teachers to quality teachers, than f(x)=[5(x/5)]/[2^(x-3)] ; where x=5 . This function holds true for the given value of x, but I doubt it will hold true for others.
  • Keivan is one of those quality teachers. Very confident in his presentation, and lucid while proof'ing . I took the class for half a semester last year, and I did not understand integration by parts then, but his explanation was spot on! This statement remains true for other topics covered also. He also does a nice job of bringing in other topics of mathematics that we will see later if we continue on i.e. things we could expect to see in differential equations, or which topics covered will be useful for different majors. This foreshadowing helps give meaning to what we are currently studying. The only area in which I think was below par was when Keivan lost a bit of his stamina at the end of the semester. This, however, I CAN NOT blame him for. Quality lectures are hard to prepare, and this becomes more difficult to do during a summer session when so much is covered so fast. Keivan did a great job remaining consistant for the most part. Overall I'm impressed and would recommend him to anyone taking math courses. His commitment and quality of lecture would help any budding-math student.
  • Mr.Monfared was a very good, polite and organized teacher. I very much enjoyed the Calculus II class this summer. Mr. Monfared covered the material very well for the amount of time he was given, and I greatly appreciated his instruction.
• Algebra and Trigonometry (MATH 1450 - Fall 2011)
• Elementary Linear Algebra (MATH 2250 - Summer 2011)
• Finite Mathematics (MATH 1050 - Spring 2011)
• Trigonometry (MATH 1405 - Fall 2010)
• Finite Mathematics (MATH 1050 - Summer 2010)
• College Algebra (MATH 1400 - Spring 2010)
• Trigonometry (MATH 1405 - Fall 2009)

• Newton's method + Animation
> Description
Use Newton's method to approximate a root of a function with animation.

> Output

	Initial Guess:   3.0000000000000000
	Next Guess:      1.6666666666666667
	Next Guess:      1.1333333333333333
	Next Guess:      1.0078431372549019
	Next Guess:      1.0000305180437934
	Next Guess:      1.0000000004656613
	An estimate of the root is   1.0000000004656613
						




> Code

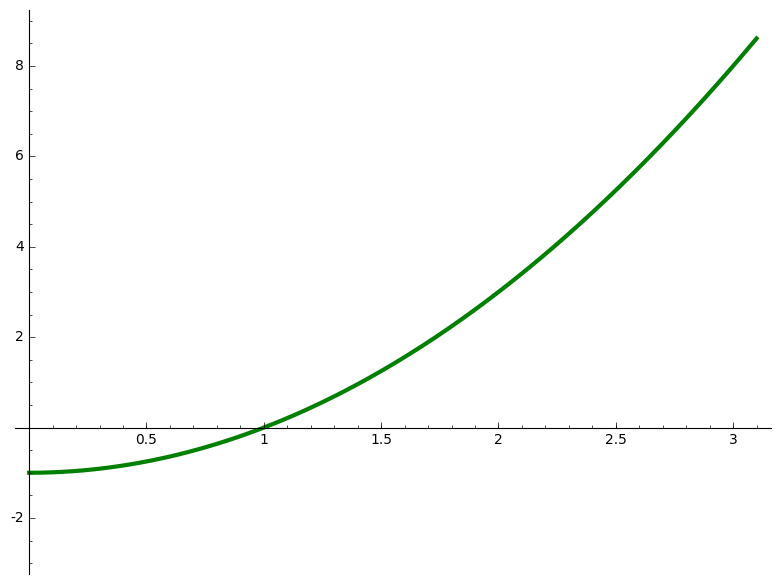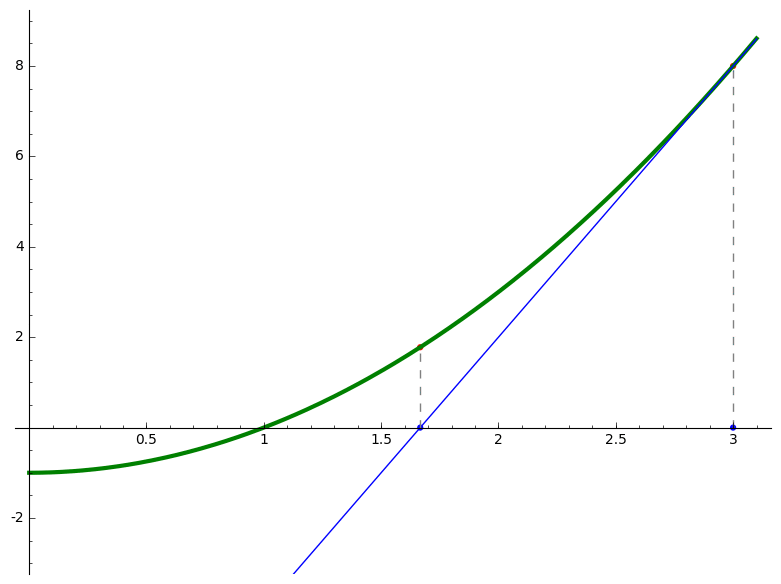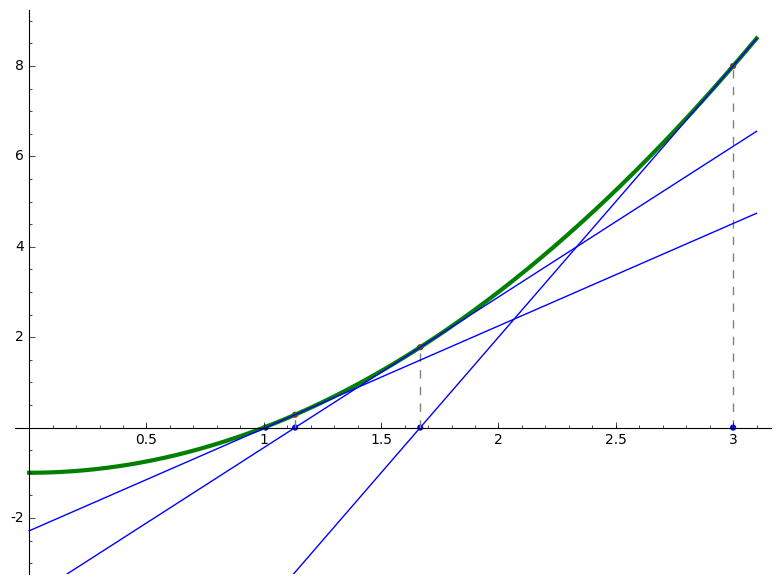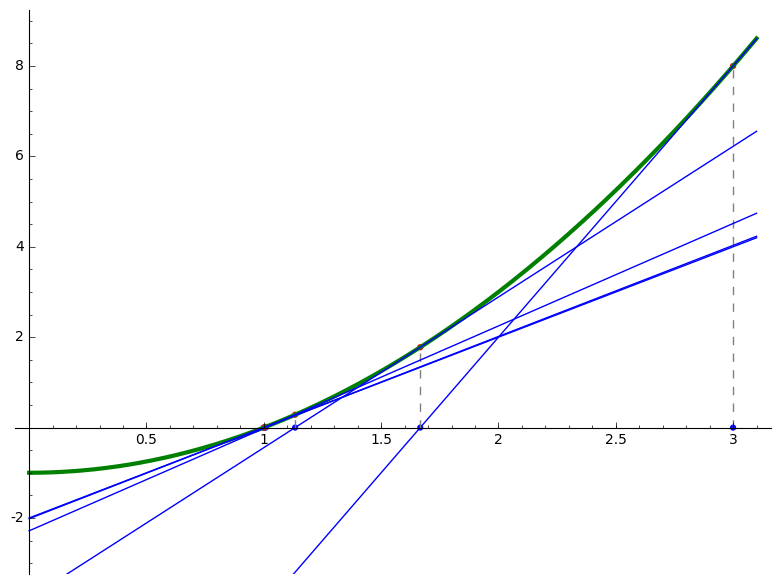
	# Use Newton's method to approximate a root of a function with animation
	var('x')

	f(x) = x^2 - 1

	xmin = 0
	xmax = 3.1
	ymin = -3
	ymax = 9
	guess = 3
	fprime = f.derivative(x)
	g(x) = x-f(x)/fprime(x)
	N = 5
	Sguess = [guess]
	print "Initial Guess: %20.16f"%(guess)
	P = plot(f(x), (xmin,xmax), ymin= ymin, ymax= ymax,color = "green",thickness=3)
	Frames = [P]

	for i in range(0,N):
		P += plot(point((guess,0),size = 20,rgbcolor=(0, 0, 1)))
		Frames += [P]
		
		P += line([(guess,0),(guess,f(guess))], color="gray", linestyle="dashed")
		Frames += [P]
		
		P += plot(point((guess,f(guess)),size = 20,rgbcolor=(1, 0, 0)))
		Frames += [P]
		
		h = f(guess) + fprime(guess)*(x-guess)
		P += plot(h, (xmin,xmax),ymin= ymin, ymax= ymax, color = "blue")
		Frames += [P]
		
		Nguess = g(guess)
		print "Next Guess:    %20.16f"%(Nguess)
		Sguess += [Nguess]
		guess = Nguess.n(digits=15)

	print "An estimate of the root is %20.16f"%(Sguess[N])

	a = animate(Frames)
	a.show(delay=100)
						



• Newton's method
> Description
Just the calculation part of the Newton's method as a function without animation in order to save time.

> Output

	Initial Guess:   9.0000000000000000
	Next Guess:      7.6666666666666670
	Next Guess:      7.5507246376811601
	Next Guess:      7.5498344877465300
	Next Guess:      7.5498344352707498
	Next Guess:      7.5498344352707498
	An estimate of the root is   7.5498344352707498
						


> Code

	# Use Newton's method to approximate a root of a function

	def Newtons_method(f,a,n):
		var('x')
		f(x) = f
		guess = a
		fprime = f.derivative(x)
		g(x) = x-f(x)/fprime(x)
		N = n
		Sguess = [guess]
		print "Initial Guess: %20.16f"%(guess)
		for i in range(0,N):
		    Nguess = g(guess)
		    print "Next Guess:    %20.16f"%(Nguess)
		    Sguess += [Nguess]
		    guess = Nguess.n(digits=15)

		print "An estimate of the root is %20.16f"%(Sguess[N])

	# Usage:
	Newtons_method(x^2-57,9,5)
						



• Plot with level curves
> Description
Plot a surface with its level curves.

> Output



> Code

	# Plot 3D with level curves

	var('x,y,z') 
	f = x^2 + y^2
	R = 4
	sum([implicit_plot3d(f==level,(x,-R,R),(y,-R,R),(z,level,level+0.1),frame=False) for level in srange(0,16,2)]+[implicit_plot3d(f==z,(x,-R,R),(y,-R,R),(z,-1,16),color='khaki',opacity=0.7,frame=False)])
						



• Plot with \(y\)-cross-sections
> Description
Plot a 3D surface with its \(y\)-cross-sections.

> Output



> Code

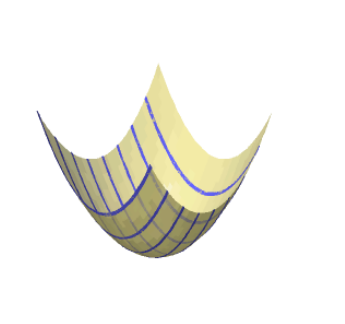
	# Plot 3D with y-cross sections

	var('x,y,z') 
	f = x^2 + y^2
	R = 4
	sum([plot3d(f,(x,-R,R),(y,level,level+0.1),frame=False) for level in srange(-R,R,1)]+[implicit_plot3d(f==z,(x,-R,R),(y,-R,R),(z,-1,32),color='khaki',opacity=0.7,frame=False)])
						



• Linearization with Jacobian matrix
> Description
The code takes a function \(f\) that maps \(\mathbb{R}^2\) to \(\mathbb{R}^2\) and draws three regions:
• the unit cube in blue,
• the image of the unit cube under \(f\) in red, and
• the linearization of the image by Jacobian of \(f\) at the origin

> Output



> Code

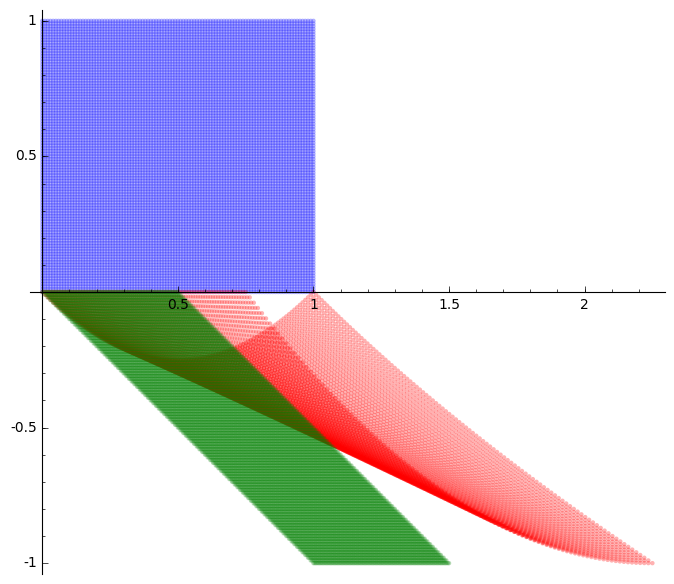
	def show_linearization(f,n=100):
		# f is a function that maps R^2 to R^2 for example
		# f(x,y) = ((x^2+2*(x+2)*(y+1))/4-1,y^2-(x+1)*y)
		# The output is three areas:
		    # the unit cube
		    # the image of unit cube under f
		    # the linearization of the image using the Jacobian of f at (0,0)
		
		var('x y')
		A = jacobian(f,(x,y))(0,0)
		p = f(0,0)
		domxy = []
		imgxy = []
		jacxy = []
		for i in range(n+1):
		    for j in range(n+1):
		        domxy.append((i/n,j/n))
		        imgxy.append(f(i/n,j/n))
		        jacxy.append(p+A*vector([i/n,j/n]))
		        
		P = points(domxy,color="blue",aspect_ratio=1, alpha = .3)
		Q = points(imgxy,color="red",aspect_ratio=1, alpha = .3)
		R = points(jacxy,color="green",aspect_ratio=1, alpha = .3)
		
		(P+Q+R).show()

	f(x,y) = ((x^2+2*(x+2)*(y+1))/4-1,y^2-(x+1)*y)
	show_linearization(f)
						



• Interactive Linear Approximation
> Description
For a given function \(f(x)\) around a point \(a\), if you zoom in close enough on the graph of the function, you can’t tell the difference between the curve and the tangent line to the graph of the function at point a. This is the basic idea for linear approximations. Actually you need to run it in sage (click on the link) to be able to interact with it.

> Output



> Code

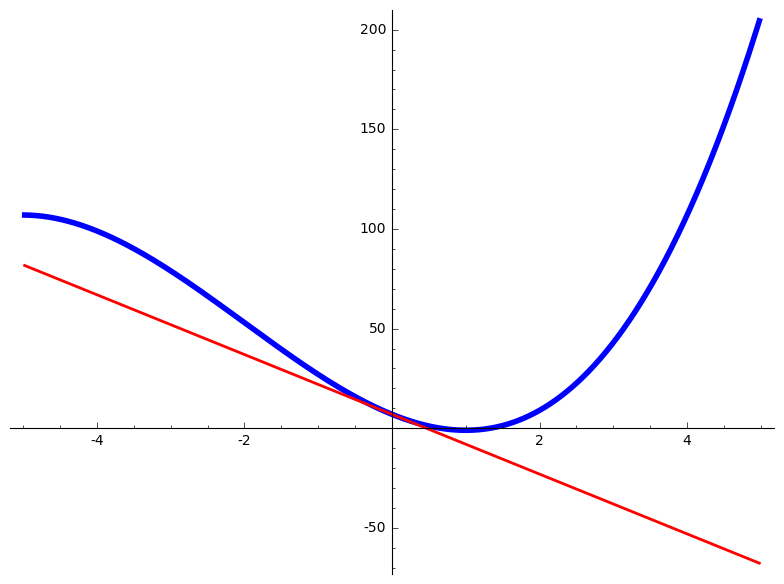
	@interact
	def _(
		f = ('$f(x)=$', input_box(x^3 + 6*x^2 - 15*x + 7,width=20)),
		a = ('around the point $x = a$', input_box(0,width=10)),
		zoom = ('zoom', slider(.1,12,default=1))):
		
		g(x) = f(a) + diff(f,x)(a)*(x-a)
		P = plot(f,(x,a-10*2^(-zoom), a+10*2^(-zoom)),  color="blue", axes=True, thickness=4) 
		# for horizontal tangent lines add 'aspect_ratio=1' to see something meaningful, 
		# otherwise sage will just change the ration so that the graph is not just a horizontal line.
		Q = plot(g,(x,a-10*2^(-zoom), a+10*2^(-zoom)),  color="red", axes=True, thickness=2)
		show(P + Q)
						



• Interactive Taylor Polynomial
> Description
The linear approximations have errors. One way to get better approximations is by taking into account the higher order derivatives of the function at the given point. This code will calculate and draw the n-th degree Taylor polynomial of the function so that you can compare them. You need to run it in sage (click on the link) to be able to interact with it.

> Output



> Code

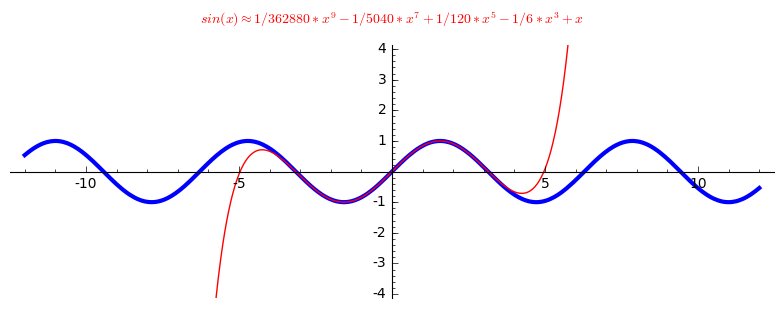
	@interact
	def _(
		f = ('$f(x)=$', input_box(sin(x),width=20)),
		n = ('Degree of the Taylor polynomial, $n=$', slider([0..9],default=3)),
		a = ('around the point $x = a$', input_box(0,width=10)),
		xzoom = ('range of $x$', range_slider(-12,12,default=(-12,12))),
		yzoom = ('range of $y$', range_slider(-20,20,default=(-4,4)))):
		
		g = f.taylor(x, a, n)
		P = plot(f,(x,xzoom[0], xzoom[1]), ymin = yzoom[0], ymax = yzoom[1],\
		         color="blue", axes=True, aspect_ratio=1, thickness=3)
		Q = plot(g,(x,xzoom[0], xzoom[1]), ymin = yzoom[0], ymax = yzoom[1],\
		         color="red", axes=True, aspect_ratio=1)
		R = text(r"$%s \approx %s$" %(f,g),(0,yzoom[1]+1),rgbcolor=(1,0,0))
		show(P + Q + R)
						

• Solving a system of linear equations (using numpy)
> Description
Given the coeeficients matrix \(A\) and the constants \(b\) this solves the system of linear equations \(Ax=b\)

> Output

	array([[-2.77777778],
		   [ 2.55555556],
		   [-0.11111111]])
						


> Code

	from numpy import linalg
	A = matrix([[1,2,3],[4,5,6],[7,8,0]])
	b = matrix([[2],[1],[1]])
	x = linalg.solve(A,b)
	x
						



• Generate random echelonizable matrix
> Description
One of the problems in teaching linear algebra is coming up with a handful of examples of matrices that can 'nicely' be row-reduced. One way to do this is to start with your 'nice' row-reduced matrix and multiply it by a few (or many) 'nice' elementary matrices and there is your example. So, one might want to code this in sage, but it's actually already done. Here is a sample. The first matrix is the randomly generated matrix with integer entries whose reduced row echelon form will also have integer entries, and the second matrix is its reduced row echelon form.

> Output



> Code

	# This code generates a random matrix A of given size and rank, which its rref form is "nice". The second matrix is the echoln form of A

	A = random_matrix(ZZ,4,5,algorithm='echelonizable',rank=3, upper_bound=5)
	show(A)
	show(A.rref())
						



• Generate random invertible matrix
> Description
Though a random matrix is invertible with probability one, for pedagogical reasons one might need a matrix with integer entries whose inverse also has integer entries. It is easy to see that for a matrix \(A\) with integer entries to have an inverse with integer entries, it is necessary that its determinant is \(\pm 1\). It turns out that it is the sufficient condition too, surprisingly, thanks to Cramer's rule! Although it might lose some pedagogical purposes, like relating the inverse to the determinant, this code generates random matrices with integer entries where their inverses also have integer entries.

> Output



> Code

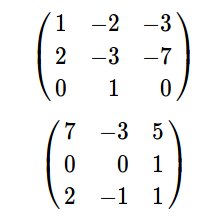
	# This generates a random matrix of given size with integer entries where the inverse also has integer entries. 
	# It can be shown that for this to happen it is necessary and sufficient that the determinant of the matrix is 1 or -1.
	# The first matrix is the random generated matrix, and the second one is its inverse

	A = random_matrix(ZZ,3,algorithm='unimodular',upper_bound=9)
	show(A)
	show(A.inverse())
						



• Step-by-step Gaussian Elimination
> Description
Does step-by-step Gauss-Jordan elimination process, and actually tells you what to do in each step.

> Output



> Code

	# Naive Gaussian reduction
	def gauss_method(MATRIX,rescale_leading_entry='Last'):
		"""Describe the reduction to echelon form of the given matrix of rationals.

		MATRIX  matrix of rationals   e.g., M = matrix(QQ, [[..], [..], ..])
		rescale_leading_entry='First' make the leading entries to 1's while doing Gaussian elimination
		rescale_leading_entry='Last' (Default) make the leading entries to 1's while reducing

		Returns: reduced form.  Side effect: prints steps of reduction.

		"""
		M = copy(MATRIX)
		num_rows=M.nrows()
		num_cols=M.ncols()
		show(M.apply_map(lambda t:t.full_simplify()))

		col = 0   # all cols before this are already done
		for row in range(0,num_rows): 
		    # ?Need to swap in a nonzero entry from below
		    while (col < num_cols
		           and M[row][col] == 0): 
		        for i in M.nonzero_positions_in_column(col):
		            if i > row:
		                print " swap row",row+1,"with row",i+1
		                M.swap_rows(row,i)
		                show(M.apply_map(lambda t:t.full_simplify()))
		                break     
		        else:
		            col += 1

		    if col >= num_cols:
		        break

		    # Now guaranteed M[row][col] != 0
		    if (rescale_leading_entry == 'First'
		       and M[row][col] != 1):
		        print " take",1/M[row][col],"times row",row+1
		        M.rescale_row(row,1/M[row][col])
		        show(M.apply_map(lambda t:t.full_simplify()))
		        
		    for changed_row in range(row+1,num_rows):
		        if M[changed_row][col] != 0:
		            factor = -1*M[changed_row][col]/M[row][col]
		            print " take",factor,"times row",row+1,"plus row",changed_row+1 
		            M.add_multiple_of_row(changed_row,row,factor)
		            show(M.apply_map(lambda t:t.full_simplify()))
		    col +=1

		print "Above is a row echelon form, let's keep cruising to get the reduced row echelon form:\n"
		
		for i in range(num_rows):
		    row = num_rows-i-1
		    if M[row] != 0:
		        for col in range(num_cols):
		            if M[row,col] != 0:
		                if M[row,col] != 1:
		                    print " take",1/M[row][col],"times row",row+1
		                    M.rescale_row(row,1/M[row][col])
		                    show(M.apply_map(lambda t:t.full_simplify()))
		                break

		        for changed_row in range(row):
		            factor = -1 * M[row-1-changed_row,col]
		            if factor != 0:
		                print " take", factor,"times row", row+1, "plus row", row-1-changed_row+1
		                M.add_multiple_of_row(row-1-changed_row,row,factor)
		                show(M.apply_map(lambda t:t.full_simplify()))
		return(M.apply_map(lambda t:t.full_simplify()))


	## Usage:
	M = matrix(SR,[[3,-1,4,6],[0,1,8,0],[-2,1,0,-4]])
	gauss_method(M,rescale_leading_entry='First')
						



• Step-by-step inverting
> Description
Inverts a matrix step-by-step by doing Gauss-Jordan elimination on the matrix augmented with the identity of the same size, and actually tells you what to do in each step.

> Output



> Code

	# Naive Gaussian reduction
	def gauss_method(MATRIX,rescale_leading_entry='Last'):
		"""Describe the reduction to echelon form of the given matrix of rationals.

		MATRIX  matrix of rationals   e.g., M = matrix(QQ, [[..], [..], ..])
		rescale_leading_entry='First' make the leading entries to 1's while doing Gaussian elimination
		rescale_leading_entry='Last' (Default) make the leading entries to 1's while reducing

		Returns: reduced form.  Side effect: prints steps of reduction.

		"""
		M = copy(MATRIX)
		num_rows=M.nrows()
		num_cols=M.ncols()
		show(M.apply_map(lambda t:t.full_simplify()))

		col = 0   # all cols before this are already done
		for row in range(0,num_rows): 
		    # ?Need to swap in a nonzero entry from below
		    while (col < num_cols
		           and M[row][col] == 0): 
		        for i in M.nonzero_positions_in_column(col):
		            if i > row:
		                print " swap row",row+1,"with row",i+1
		                M.swap_rows(row,i)
		                show(M.apply_map(lambda t:t.full_simplify()))
		                break     
		        else:
		            col += 1

		    if col >= num_cols:
		        break

		    # Now guaranteed M[row][col] != 0
		    if (rescale_leading_entry == 'First'
		       and M[row][col] != 1):
		        print " take",1/M[row][col],"times row",row+1
		        M.rescale_row(row,1/M[row][col])
		        show(M.apply_map(lambda t:t.full_simplify()))
		        
		    for changed_row in range(row+1,num_rows):
		        if M[changed_row][col] != 0:
		            factor = -1*M[changed_row][col]/M[row][col]
		            print " take",factor,"times row",row+1,"plus row",changed_row+1 
		            M.add_multiple_of_row(changed_row,row,factor)
		            show(M.apply_map(lambda t:t.full_simplify()))
		    col +=1

		print "Above is a row echelon form, let's keep cruising to get the reduced row echelon form:\n"
		
		for i in range(num_rows):
		    row = num_rows-i-1
		    if M[row] != 0:
		        for col in range(num_cols):
		            if M[row,col] != 0:
		                if M[row,col] != 1:
		                    print " take",1/M[row][col],"times row",row+1
		                    M.rescale_row(row,1/M[row][col])
		                    show(M.apply_map(lambda t:t.full_simplify()))
		                break

		        for changed_row in range(row):
		            factor = -1 * M[row-1-changed_row,col]
		            if factor != 0:
		                print " take", factor,"times row", row+1, "plus row", row-1-changed_row+1
		                M.add_multiple_of_row(row-1-changed_row,row,factor)
		                show(M.apply_map(lambda t:t.full_simplify()))
		return(M.apply_map(lambda t:t.full_simplify()))


	## Usage:
	M = matrix(SR,[[3,-1],[2,1]])
	R = gauss_method(M.augment(identity_matrix(M.ncols()),subdivide=True))
						



• Step-by-step inverting a generic \(2\times 2\) matrix
> Description
Inverts a generic \(2\times 2\) matrix step-by-step by doing Gauss-Jordan elimination on the matrix augmented with the identity of the same size, and actually tells you what to do in each step. You can do the same on a \(3\times 3\) or larger matrix by doing a similar process. like below:

	var('a b c d e f g h i j k l m n o p q r s t u v w x y z')
	A = matrix([[a,b,c],[d,e,f],[g,h,k]])
	R = gauss_method(A.augment(identity_matrix(A.ncols()),subdivide=True))
	

And then you can see the final result by reading only the augmented part:

	view(R.subdivision(0,1))
	

Of course it's going to look a little ugly, so you might want to first multiply it by the determinant of the original matrix and then simplify it:

	view((det(A)*R.subdivision(0,1)).apply_map(lambda t:t.full_simplify()))
	


> Output



> Code

	# Naive Gaussian reduction
	def gauss_method(MATRIX,rescale_leading_entry='Last'):
		"""Describe the reduction to echelon form of the given matrix of rationals.

		MATRIX  matrix of rationals   e.g., M = matrix(QQ, [[..], [..], ..])
		rescale_leading_entry='First' make the leading entries to 1's while doing Gaussian elimination
		rescale_leading_entry='Last' (Default) make the leading entries to 1's while reducing

		Returns: reduced form.  Side effect: prints steps of reduction.

		"""
		M = copy(MATRIX)
		num_rows=M.nrows()
		num_cols=M.ncols()
		show(M.apply_map(lambda t:t.full_simplify()))

		col = 0   # all cols before this are already done
		for row in range(0,num_rows): 
		    # ?Need to swap in a nonzero entry from below
		    while (col < num_cols
		           and M[row][col] == 0): 
		        for i in M.nonzero_positions_in_column(col):
		            if i > row:
		                print " swap row",row+1,"with row",i+1
		                M.swap_rows(row,i)
		                show(M.apply_map(lambda t:t.full_simplify()))
		                break     
		        else:
		            col += 1

		    if col >= num_cols:
		        break

		    # Now guaranteed M[row][col] != 0
		    if (rescale_leading_entry == 'First'
		       and M[row][col] != 1):
		        print " take",1/M[row][col],"times row",row+1
		        M.rescale_row(row,1/M[row][col])
		        show(M.apply_map(lambda t:t.full_simplify()))
		        
		    for changed_row in range(row+1,num_rows):
		        if M[changed_row][col] != 0:
		            factor = -1*M[changed_row][col]/M[row][col]
		            print " take",factor,"times row",row+1,"plus row",changed_row+1 
		            M.add_multiple_of_row(changed_row,row,factor)
		            show(M.apply_map(lambda t:t.full_simplify()))
		    col +=1

		print "Above is a row echelon form, let's keep cruising to get the reduced row echelon form:\n"
		
		for i in range(num_rows):
		    row = num_rows-i-1
		    if M[row] != 0:
		        for col in range(num_cols):
		            if M[row,col] != 0:
		                if M[row,col] != 1:
		                    print " take",1/M[row][col],"times row",row+1
		                    M.rescale_row(row,1/M[row][col])
		                    show(M.apply_map(lambda t:t.full_simplify()))
		                break

		        for changed_row in range(row):
		            factor = -1 * M[row-1-changed_row,col]
		            if factor != 0:
		                print " take", factor,"times row", row+1, "plus row", row-1-changed_row+1
		                M.add_multiple_of_row(row-1-changed_row,row,factor)
		                show(M.apply_map(lambda t:t.full_simplify()))
		return(M.apply_map(lambda t:t.full_simplify()))


	## Usage:
	var('a b c d')
	A = matrix([[a,b],[c,d]])
	R = gauss_method(A.augment(identity_matrix(A.ncols()),subdivide=True))
						



• Draw Gershgorin disks
> Description
Gershgorin circle theorem roughly states that the eigenvalues of an \(n \times n\) matrix lie inside \(n\) circles where \(i\)-th circle is centred at \(A_{i,i}\) and its radius is the sum of the absolute values of the off-diagonal entries of the \(i\)-th row of \(A\). Applying this to \(A^{\top}\) implies that the radius of this circles shall be the smaller of the sums for rows and columns. This Sage code draws the circles for a given matrix.

> Output



> Code

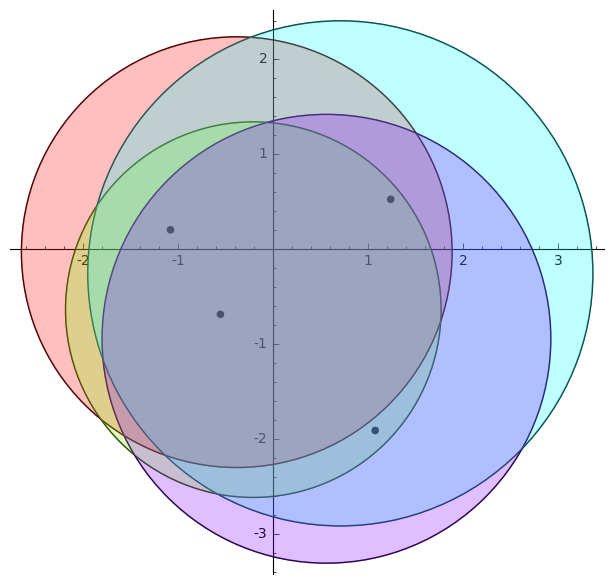
	def Gershgorin(A,evals=False):
		# A is a square matrix
		# Output is the Gershgorin disks of A
		
		from sage.plot.circle import Circle
		from sage.plot.colors import rainbow
		
		n = A.ncols()
		Colors = rainbow(n, 'rgbtuple')
		E = point([])
		
		B = A.transpose()
		R = [(A[i-1,i-1], min(sum( [abs(a) for a in (A[i-1:i]).list()] )-abs(A[i-1,i-1]),\
		                      sum( [abs(a) for a in (B[i-1:i]).list()] )-abs(B[i-1,i-1])))\
		     for i in range(1,n+1)]
		C = [ circle((real(R[i][0]),imaginary(R[i][0])), R[i][1], color="black") for i in range(n)]
		if evals == True:
		    E = point(A.eigenvalues(), color="black", size=30)
		CF = [ circle((real(R[i][0]),imaginary(R[i][0])), R[i][1], rgbcolor=Colors[i],\
		              fill=True, alpha=1/n) for i in range(n)] 
		
		(sum(C)+sum(CF)+E).show()
		
	## Usage:
	A =  random_matrix(CDF,4,)
	Gershgorin(A,evals=True)
						

• A full matrix with given eigenvalues
• On the last digits of consecutive prime numbers
• Multiplication graph

• Learning is done by doing and sharing
and this can be achieved when learners are actively and independently engaged in a learning process, and when they can share this experience together. Traditionally, mathematics is taught as mostly lecture. In my classes I use a mix of strategies. For instance, in some of my classes I give only short lectures at the beginning of each day, or some days I do not lecture at all. Instead, students are given worksheets that include problems that are arranged from basic one-step questions to more involved computational and conceptual problems. Students form groups that they stay with for a portion of the semester, and they work on the worksheets in their groups. I attend each group and answer their questions and direct their discussions. Sometimes that I feel necessary, I give a mini lecture for the class, or solve one of the problems on the board, and then I let the group discussions continue. At the end of the day I post the solutions online, where the students can access them after they are ready for it. Often students come to me at the end of a class to tell me that they liked the time when they could get their hands dirty on a problem during the class, and usually they ask for more such opportunities. I have seen those "ahha!" moments happening in class when students ask a question from a group-mate and get responses from them, or when they discover new concepts or identify a common mistake together. Some of them have told me that they learned a topic when they taught it to a classmate. A few years ago I taught two linear algebra courses, one lecture based, and one using the method I described here. The response rate to my in-class questions in the second method was much higher, and the students overall performed better in the exams. I am currently working on how to incorporate these activities in larger classrooms.
• Motivation is the key
Learners are strongly encouraged when the teacher is passionate about the subject and is respectful of the learners. A common comment that I receive from my students is that my excitement about teaching a topic made them interested in learning about it. As a result they paid more attention to it in class, asked more questions, and got actively engaged in learning as they made connections between their life or disciplines and the topic being discussed. I motivate a lot of topics in mathematics and statistics with real life applications. For example, in a linear algebra course I explain how google uses "eigenvectors" to sort the search results, or how instagram applies certain filters on images using "projections". In a statistics course, I use various games such as "plinko" to motivate topics. Often, I bring in pieces of history of mathematics and mathematicians to the discussions. I ask an open-ended question from students, and then direct them to ask more precise questions. For instance, I ask "how do you estimate the area of a potato-shaped closed curve?", and then we work together until we find better questions. Then I tell them that they would be as famous as Archimedes or even Riemann only if they were born a few hundred years ago, because they asked the same questions that they did. One of my favourite parts of teaching is getting students excited about coming up with ideas on how a lesson relates to their disciplines, how they can explain a topic to their little sibling or to their parents in a fun way, or even how to bring it up at a party. One of my challenges is to keep students motivated and active for the entire time of class. Ideally, I would love them to keep asking questions until they get to the questions that they can answer, and then work their way backwards to answer the big questions.
• Students' ways of learning matter
I constantly seek for feedback from my students. If I see them on the hallways or when we are just walking to the class, I ask them about how they feel about the course, how do they think they are performing, and what are the things that they like or do not like in the class. I also send online feedback forms to students during the semester to get an understanding of how I am doing, and often I make changes according to what the students say during the semester. One of my strategies to get an informative feedback is to explain to students the results of feedback my previous students have given. Then I report on their feedback immediately, and communicate to them how I am going to implement their suggestions. I am thinking about a sustainable way of continually getting feedback from students on a daily basis and implementing it in my classes. Also, as students need our feedback to improve, I feel I need my peers' feedback to improve. Hence, I continually seek feedback from my colleagues on my teaching. Moreover, I ask people from outside mathematics department to observe my classes so that I also see a non-mathematician's point of view on delivering methods, and not just the content.